Online Course Discussion Forum
Mock
This was in one of the mock tests.
A set of teams held a round-robin tournament in which every team played every other team exactly once. Every team won ![]() games and lost
games and lost ![]() games; there were no ties. How many sets of three teams
games; there were no ties. How many sets of three teams ![]() were there in which
were there in which ![]() beat
beat ![]() ,
, ![]() beat
beat ![]() , and
, and ![]() beat
beat ![]()
I don't get how to do it.
Hi Tina, this question is a pretty interesting one.
To start, we need to figure out how many teams there are. Since each team won 10 and lost 10 games, there must be 21 teams in total.
Hence, there are $\binom{21}{3} = 1330$ sets of three teams in total.
We want to count how many of these sets have each team beating another team in the group of 3.
Here's a hint for how to proceed. Note that in ANY of these sets of 3 teams, either (i) one team beats the other two teams (what we don't want) or (ii) each team beats another team (what we want) and no other outcome is possible. These are roughly shown in the picture below (where an arrow denotes a team beating another):
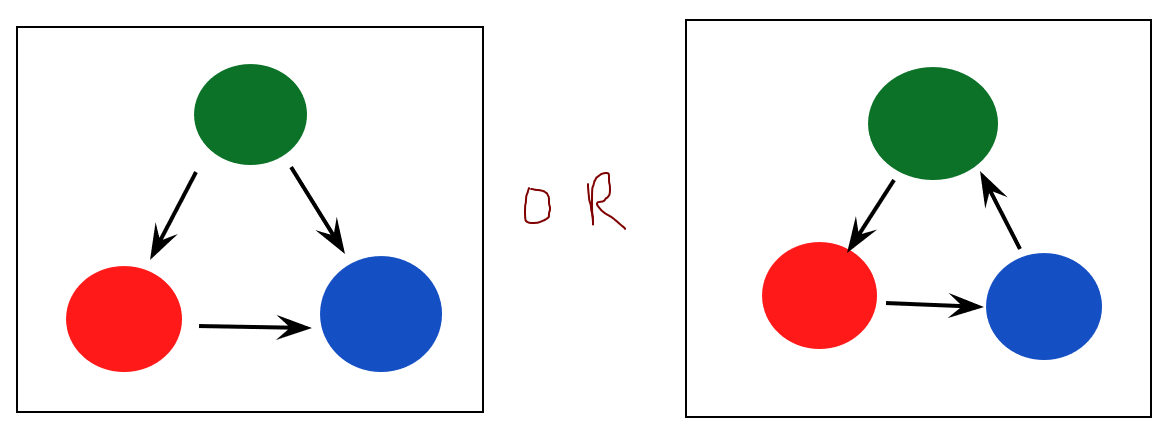
Therefore, if you can count the number of outcomes in possibility (i) on the left, then you can subtract that number from the total. Be a little careful, remember the set of three is chosen in no particular order.
Give this a try and let us know if you have additional questions. The fact that each team won 10 games will probably be needed again here.
Social networks