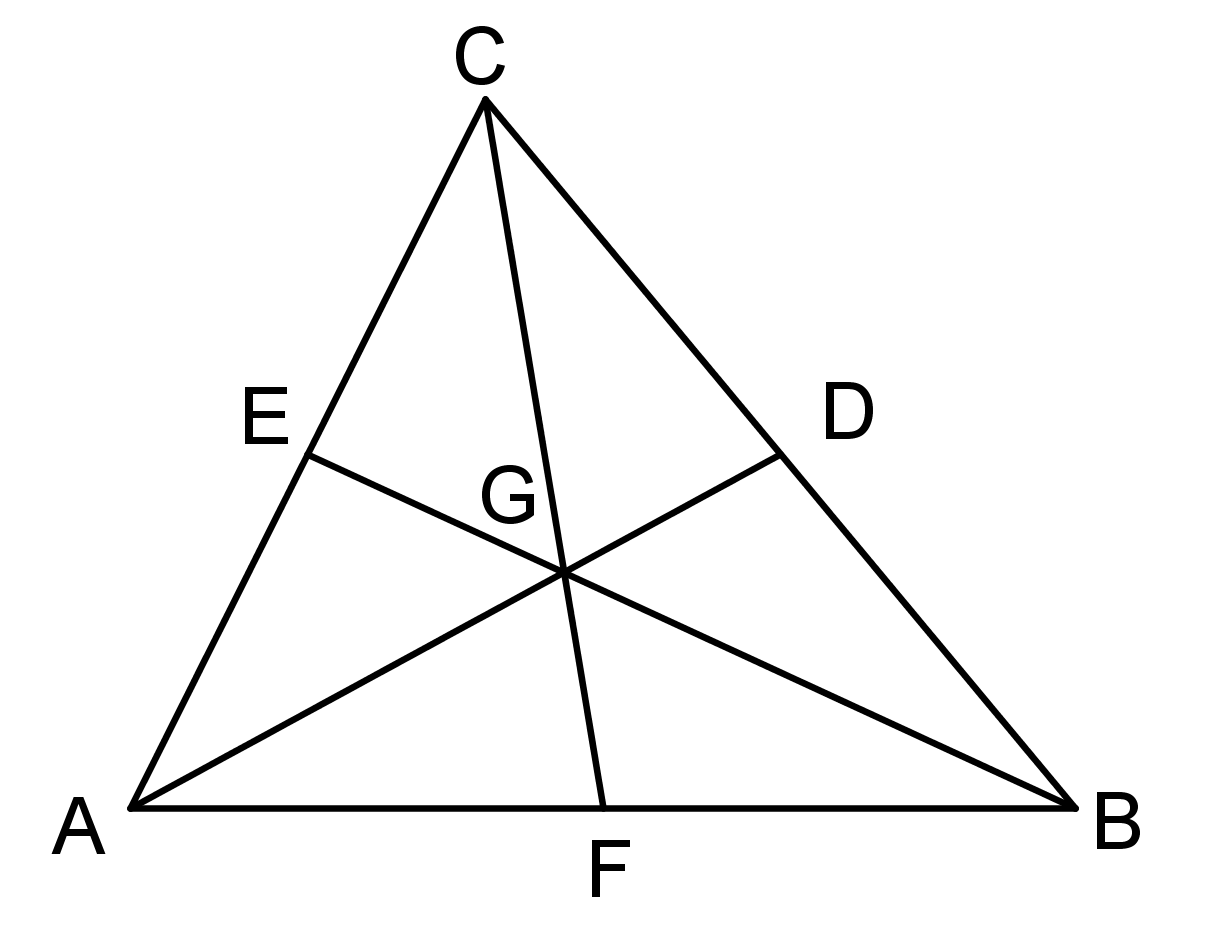
One of the questions we didn't get to in class was Example 4.7 about the centroid of a triangle.

Remember that the centroid is the point where all the medians meet in a triangle. In the diagram below, D, E, F are all midpoints, and G is the centroid:

4.27 on the homework is to show the centroid always exists (using areas), but we'll also see the more classical proof next week in class.

For 4.7, just take for granted this point exists. We want to show that $AG:GD = BG:GE=CG:GF=2:1$. We'll just show $CG:GF= 2:1$ (the others are identical). The key fact we'll use over and over is that for triangles the ratio of areas that share the same height is the ratio of the bases.

Using the line $BC$ as a base, note $[ADC]=[ADB]$ and $[GDC]=[GDB]$ as $D$ is the midpoint. Hence subtracting these areas we get $[AGC]=[AGB]$. (This should hopefully remind you of the trapezoid fact we ended class with.)

Now using $AB$ as a base, we have $[AGF]=[BGF]$ (using that $F$ is the midpoint) so $[AGF] = [AGB]/2 = [AGC]/2$. Hence we can finish the problem noting $$\frac{CG}{GF} = \frac{[AGC]}{[AGF]} = 2$$ as $\triangle AGC$ and $\triangle AGF$ share the same height.

The homework problem 4.27 can be done in a similar manner. The proof starts like so (an example of the "ghost point" method we briefly mentioned in class):  Instead let $G$ be the intersection of $AD$ and $BE$ (this always exists). Extend $CG$ to intersect $AB$ at $F$ (again we can always do this). Then show that $F$ is actually the midpoint (hence our "ghost point" $G$ is actually the centroid as needed).