Hi Kathy,

Sorry no one got back to you sooner.

Now that the solutions are available on the class page I'll give some comments that might help with the solutions given.

For 8.20, we use the midpoint of the base as the dividing point for the other two triangles. Therefore all three of the drawn triangles have the same base and the same height so they all have the same area (they have the same height because the two bases are parallel in a trapezoid).

For 8.22, we are first looking at what fraction of the full area $DMN$ is. The idea here is to use $[DMN] = [ABCD] - [AMD] - [CDN] - [BMN]$ to find that $[DMN]$ is $3/8$ of the entire parallelogram.

8.27 is a little tricky, that one might be a good one to review at the start of class.

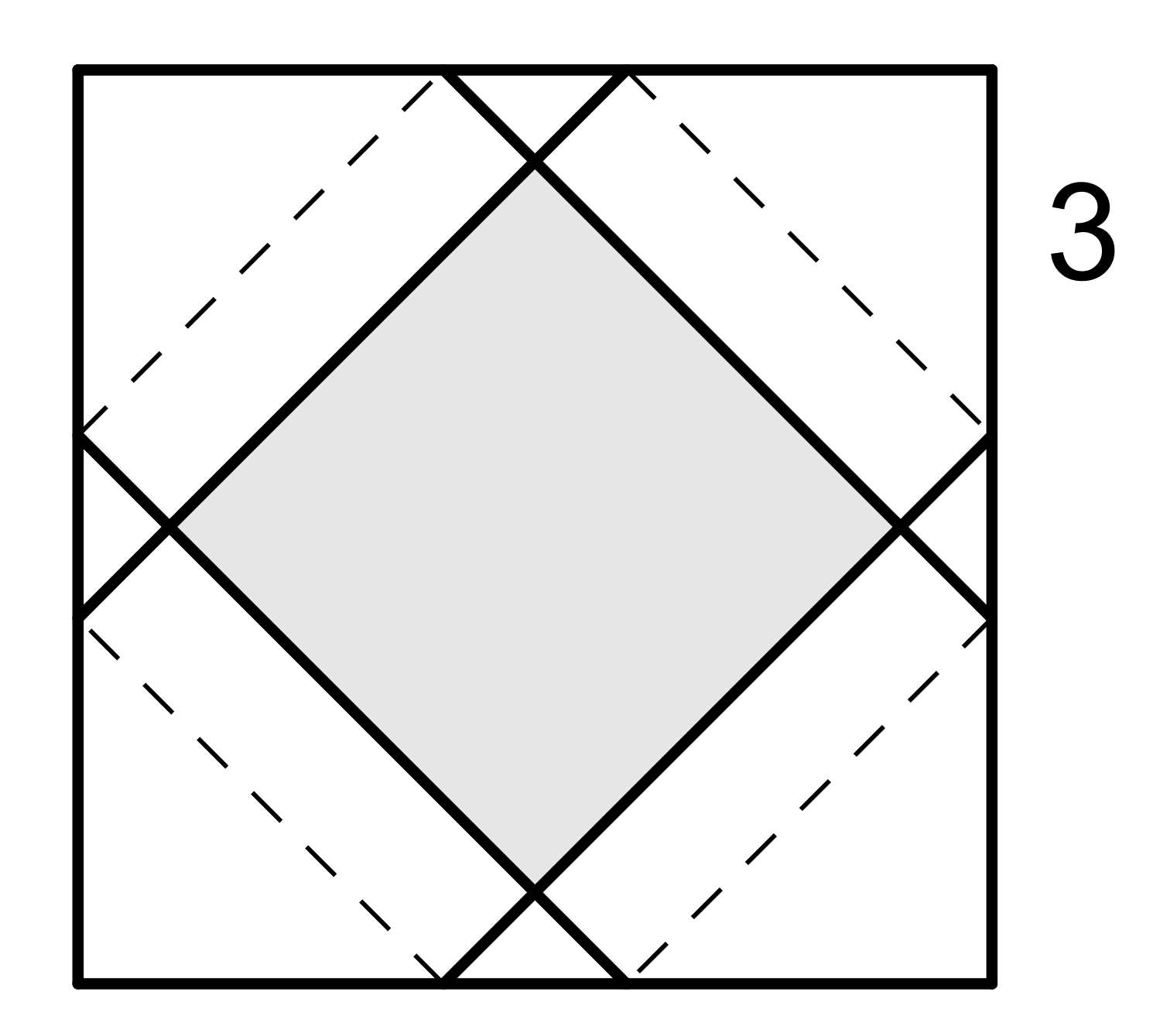
For 8.28b, the following picture may help

For 8.29, the key observation is that $[ABG]+[CDF]−[EFG]  =[ABCD]−[EBC]$. It really helps to draw this out, as we are saying if you calculate the area of triangle $ABG$ and $CDF$ and the subtract the area of triangle $EFG$ you get the same answer as calculating the area of parallelogram $ABCD$ and subtracting triangle $EBC$.

Let me know if you have more questions, I'm happy to fill in more details.