Online Course Discussion Forum
Math Challenge IV Fall 2017 Worksheet 5, Example 6
We only discussed a sketch of the solution of this problem in class. Here I post the full solution.
First, the problem:
Given $\triangle ABC$, for an arbitrary point $T$, construct perpendicular lines from $T$ to $\overline{BC}$, $\overline{CA}$, and $\overline{AB}$, with feet $T_a$, $T_b$, and $T_c$ respectively.
(a) Show that if and only if $\triangle ABC$ is an equilateral triangle,
\[
AT_c + BT_a+ CT_b = T_bA + T_cB + T_aC
\]
holds for every point $T$. Here $\overline{AT_c}$, etc. are directed segments, and define $AT_c$ to be positive if $T_c$ is on ray $\overrightarrow{AB}$, and negative if $T_c$ is on the extension of $\overline{BA}$.
(b) Show that if $\triangle ABC$ is not equilateral, then the locus of points $T$ satisfying
\[
AT_c + BT_a+ CT_b = T_bA + T_cB + T_aC
\]
is the line $\overleftrightarrow{OI}$ where $O$ and $I$ are the circumcenter and incenter of $\triangle ABC$, respectively.
Solution:
Set up rectangular coordinate system. Let the coordinates of the given points $A$, $B$, and $C$ be $(x_A, y_A)$, $(x_B, y_B)$, and $(x_C, y_C)$, respectively. These coordinates are fixed values. The equations of the sides of $\triangle ABC$ are also fixed.
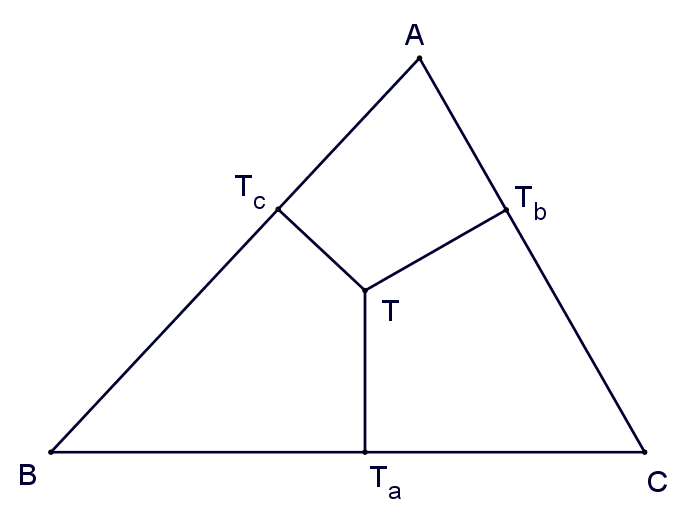
Let the coordinates of point $T$ be $(x_T, y_T)$. The line $\overline{TT_a}$ is perpendicular to $\overline{BC}$, so its slope (if exists) $k$ multiplies the slope of $\overline{BC}$ equals $-1$, so the slope is independent of $(x_T, y_T)$, and the equation is $y-y_T=k(x-x_T)$, which is $kx-y + (-kx_T + y_T) = 0$, where only the constant term depends on $(x_T,y_T)$. In the case where one of the slopes of $\overline{TT_a}$ and $\overline{BC}$ doesn't exist, it means one is horizontal and one is vertical, so the equation of $\overline{TT_a}$ is either $x=x_T$ or $y=y_T$. Overall, the equation of $\overline{TT_a}$ is $Px + Qy + R=0$, where $P$ and $Q$ do not depend on $(x_T, y_T)$, and $R=-Px_T-Qy_T$ which is a linear expression of $x_T$ and $y_T$.
The directed length of $BT_a$, which is the distance from $B$ to line $\overline{TT_a}$, can be computed with the formula
\[
BT_a = \frac{Px_B + Qx_B + R}{\sqrt{P^2+Q^2}},
\]
this is a linear expression in $x_T$ and $y_T$ as well. Similarly, we can find $AT_c$ and $CT_b$ are also linear expressions in $x_T$ and $y_T$, so the sum $AT_c+BT_a+CT_b$ is a linear expression in $x_T$ and $y_T$, i.e.
\[
AT_c+BT_a+CT_b = \alpha x_T + \beta y_T + \gamma,
\]
where $\alpha, \beta, \gamma$ are all constants independent of $x_T$ and $y_T$. Here $\alpha$ and $\beta$ are allowed to be both $0$.
The equality $AT_c + BT_a+ CT_b = T_bA + T_cB + T_aC$ is equivalent to
\[
\alpha x_T + \beta y_T + \gamma = \frac{1}{2}(AT_c + BT_a+ CT_b+ T_bA + T_cB + T_aC) = \frac{1}{2}(a+b+c) = s.
\]
Now assume $\triangle ABC$ is equilateral. We prove that the equality above holds for any point $T$ on the plane. It is easy to verify that if $T$ coincides with $A$, $B$, or $C$, the equality holds. If $T$ is an arbitrary point on the plane, the coordinates of $T$ can be expressed as (by normalized barycentric coordinates):
\[
x_T = \lambda x_A + \mu x_B + \nu x_C, \quad y_T = \lambda y_A + \mu y_B + \nu y_C,
\]
where $\lambda + \mu + \nu = 1$. Some further calculation shows that $\alpha x_T + \beta y_T + \gamma = s$ holds for arbitrary $T$ as well.
Conversely, assume the equality $\alpha x_T + \beta y_T + \gamma = s$ holds for arbitrary point $T$. So let $T$ be $A$, and let $D$ be the foot of perpendicular line from $A$ to $\overline{BC}$, then
\[
BD+CA = s.
\]
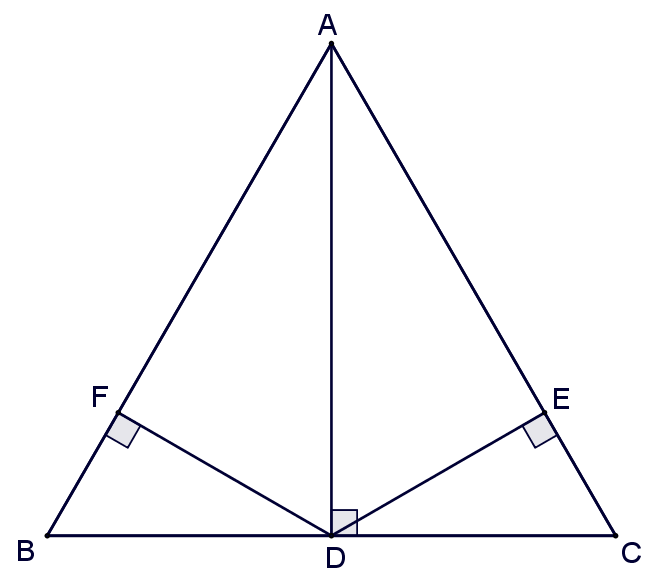
Now let $T$ be $D$, and construct $\overline{DE}$ and $\overline{DF}$ perpendicular to $\overline{AC}$ and $\overline{AB}$, with feet $E$ and $F$, respectively, then
\[
BD+CE+AF=s.
\]
Comparing the previous two equations, we get
\[
EA=AF,
\]
which means that the altitude $\overline{AD}$ is also the angle bisector of $\angle BAC$, therefore $AB=AC$.
Similarly, $AB=BC$, so $\triangle ABC$ is equilateral. This completes the proof for part (a).
Now we prove part (b): if $\triangle ABC$ is not equilateral, the circumcenter $O$ and incenter $I$ are not the same point. It is easy to verify that both $O$ and $I$ satisfy the equality
\[
\alpha x_T + \beta y_T + \gamma = s,
\]
and so does any point on the line $\overleftrightarrow{OI}$. For any point $P$ not on the line $\overleftrightarrow{OI}$, it cannot satisfy the equality above (otherwise all points on the plane would satisfy it and we have proved that that only occurs when $\triangle ABC$ is equilateral). Therefore the locus of the points with $\alpha x_T + \beta y_T + \gamma = s$ is the line $\overleftrightarrow{OI}$.
Social networks