Areteem: Math Challenge IC: Handout 8

Online Course Discussion Forum

Math Challenge IC: Handout 8

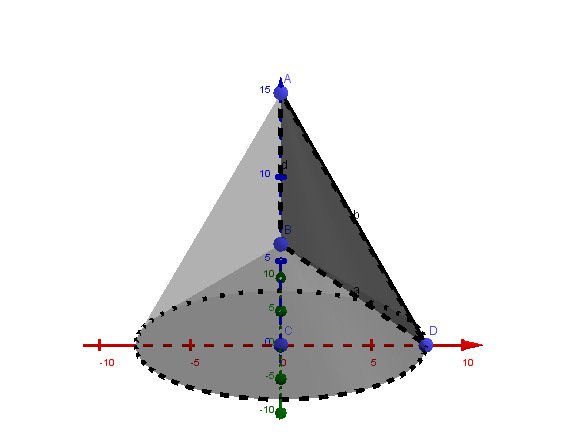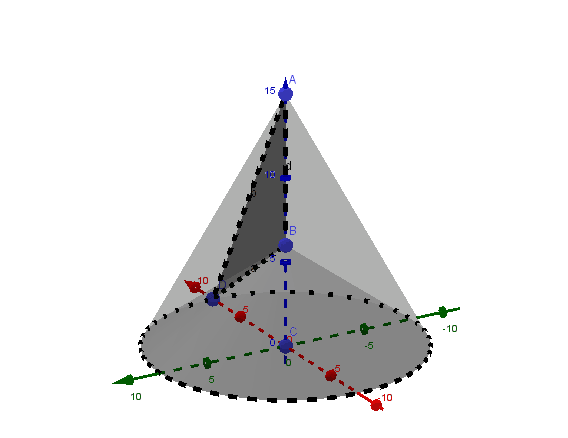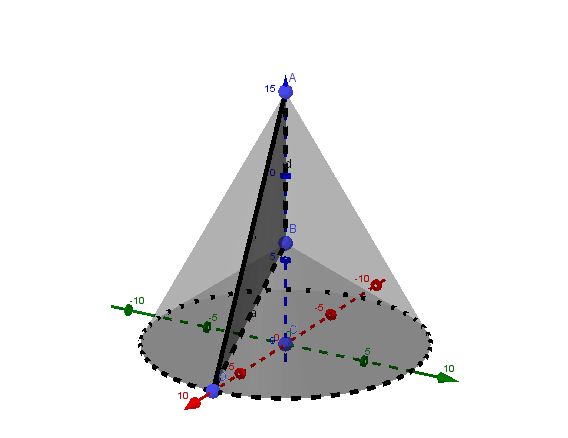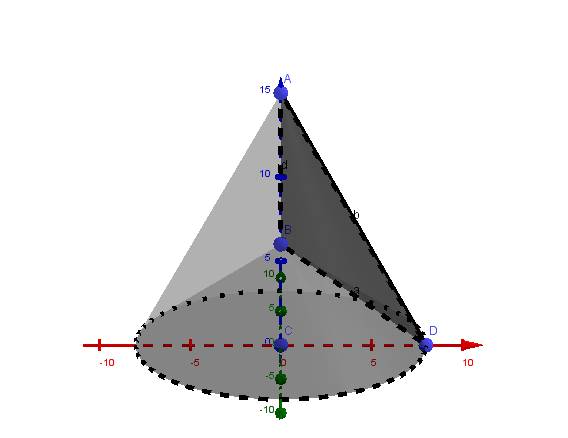
For problem 8.30, how is a flat piece of triangle "rotated about the smallest side" into a solid. In the video lecture, it has been stated that the solid is the cone minus the smaller cone on the bottom. Does that mean the solid is the two obtuse triangles at the top? If so, why is one of the triangles dotted lined?

Thank you!

If the problem instead had a right triangle with sides $3$, $4$, and $5$ and we rotate it about the side of length $4$, we would get a full cone that has radius $6$ and height $4$.

Since this is an obtuse triangle, we can think of it as a right triangle minus a smaller right triangle that has the same base, so as we rotate it, we obtain a big cone with a smaller cone removed on the bottom.

Show parent

For fun, we can see it as a gif as well, where the dark triangle is mapping out the conical shape. We want just the top part of the shape, and bottom (darker cone) is not part of the solid.

Rotation of Cone

Show parent

Thank you! The gif really helped me see it!

Show parent