Online Course Discussion Forum
reviewing homework for lesson 3 math challenge I-C questions
I'm reviewing the past lessons then I still don't really get 3.30, after I reviewed the posted solutions, also Mr. John didn't explain it in the homework discussion.
can I get some help? Thank you.
Hi Bober,
Can you maybe say a little more about what you're confused about? To start, attached below is the diagram from class yesterday (with points A,B,C,D added in)

B is the point the two cables are attached to the ground, with BD one cable and BC the other. $\angle ABD = 55^\circ$ while $\angle ABC = 75^\circ$. The problem states $CD = 3$ and we let $AD = x$ and $AB = y$. (Thus $AC = x+3$ is the height of the pole and $AB=y$ is the distance from the pole the cables are attached.
Looking at the tangent equation for $\triangle ABD$ and $\triangle ABC$ gives the two equations above for $x$ and $y$. Since $\tan(55^\circ)$ and $\tan(75^\circ)$ are numbers, we can then solve these equations for $x$ and $y$.
Let me know if you still have questions from here!
Mr. John, I'm confused about 3.30, not 4.30 sorry I didn't say it clearly.
Thank You
Sorry! It does clearly say 3.30, but it was right after we finished the chapter 4 discussion, so I was thinking of those problems.
For 3.30, we want the largest square in an equilateral triangle with side length $6$. This square (with side length $x$) will be as shown below:
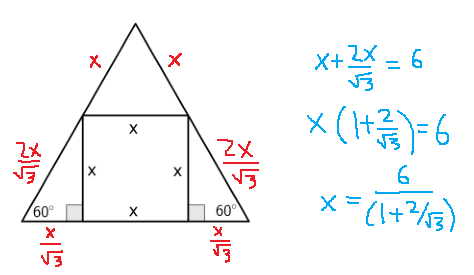
Since the square has $90^\circ$ angles, it divides the equilateral triangle into a smaller equilateral triangle, the square, and two 30-60-90 triangles. Since these 30-60-90 triangles have a ratio of sides $1 : \sqrt{3} : 2$, if the middle length is $x$, the sides are $x/\sqrt{3} : x : 2x/\sqrt{3}$. This allows us to set up a linear equation and solve for $x$, as shown above. Writing $x$ in simplest radical form gives $12\sqrt{3} - 18$.
Hope this helps a bit, otherwise let me know if there's a specific part that's confusing.
社交网络