Online Course Discussion Forum
still need additional help on p18 in winter camp geometry blue
I was not able to prove triangle BGH is identical to triangle CGE, and why HGCOHGCO is a cyclic quadrilateral. also not sure how to prove CEF is similar to EBF. thanks
Can a teacher please answer my question that was posted 5 days ago? thanks
Question:
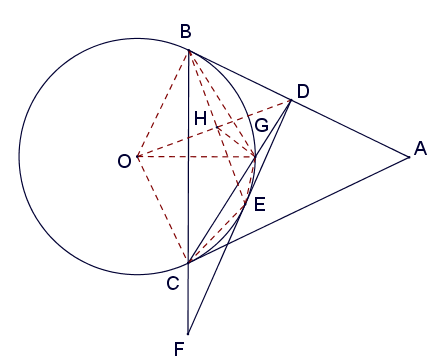
As shown in the diagram, $\overline{AB}$ and $\overline{AC}$ are two tangent lines of $\odot O$. Let $\overline{CD}$ be an angle bisector of $\triangle ABC$. Let $F$ be a point on the extension of $\overline{BC}$ such that $\overline{DF}$ is tangent to $\odot O$ at $E$. Given that $BC=21$, find $CF$.
Solution:
Let $G$ be the intersection of $\overline{CD}$ and $\odot O$, and connect $\overline{OB}$, $\overline{OC}$, $\overline{OG}$, $\overline{OD}$, $\overline{BG}$, $\overline{BE}$, and $\overline{CE}$. Let $H$ be the intersection of $\overline{BE}$ and $\overline{OD}$, and connect $\overline{HG}$, as shown in the diagram.
Since $\overline{BD}$ and $\overline{DE}$ are tangent to $\odot O$, $\overline{OD}\perp\overline{BE}$ and $H$ is the midpoint of $\overline{BE}$. Also $\angle OBD=90^\circ$, so $\triangle OBD\sim\triangle BHD$, and then $\dfrac{BD}{DH}=\dfrac{OD}{BD}$, which means $BD^2 = DH\cdot DO$.
Since $BD^2=DG\cdot DC$, we obtain \[ DH\cdot DO = DG\cdot DC, \] therefore $HGCO$ is a cyclic quadrilateral, and hence $\angle DHG=\angle DCO=\angle CGO$. Furthermore, we know that $\overline{CD}$ bisects $\angle ACB$, so $G$ is the midpoint of arc $\widehat{BC}$, then \[ \begin{split} \angle GHE=90^\circ-\angle DHG=90^\circ-DCO\\ =\angle DCA=\angle GCB=\angle GEH, \end{split} \] thus $GH=GE$. Also, \[ \angle HGE=180^\circ-2\angle GHE=180^\circ-2\angle GCB=\angle BGC, \] so \[ \angle BGH=\angle BGC-\angle HGC=\angle HGE-\angle HGC=\angle CGE. \]
Now we have $GH=GE$, $\angle BGH=\angle CGE$, and $BG=CG$, so $\triangle BGH\cong\triangle CGE$ by $SAS$ congruency. Therefore $CE=BH=\dfrac{1}{2}BE$. Since $\angle CEF=\angle EBF$, we have $\triangle CEF\sim\triangle EBF$, and \[ \frac{CF}{EF} = \frac{EF}{BF} = \frac{CE}{BE} = \frac{1}{2}, \] thus \[ \frac{CF}{BF} = \frac{1}{4}, \] therefore \[ CF=\frac{1}{3}BC=7. \]
Social networks