In the diagram below we can see the rotated triangle $\triangle BCP'$. 

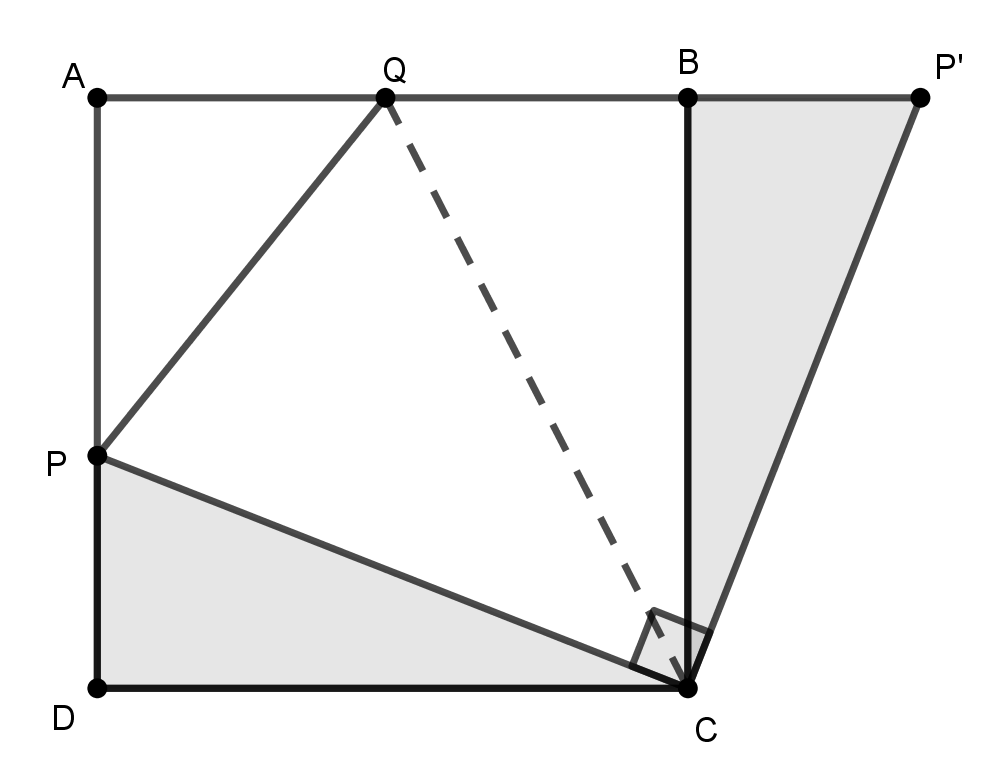
The key is noticing that since $ABCD$ is a unit square, $\triangle APQ$ has perimeter $2$, and $\triangle PDC \cong \triangle P'BC$,  $\triangle PQC \cong \triangle P'QC$:

• $PC = P'C$
• $QC = QC$
• $QP = 2 - AQ - AP = (1-AQ) + (1- AP) = QB + DP = QB + BP' = QP'$

In particular, $\angle P'CQ = \angle PCQ$. Since we rotated $90^\circ$, $\angle PCP' = 90^\circ$, and $\angle PCP' = \angle PCQ + \angle P'CQ$, so $\angle PCQ = 90^\circ \div 2 = 45^\circ$.