Following the ideas from the book for 5.10, let G be the circumcenter and O be the circumcenter. Let H be on ray OG so that OG : GH = 1 : 2. We want to show that H is actually the altitude.

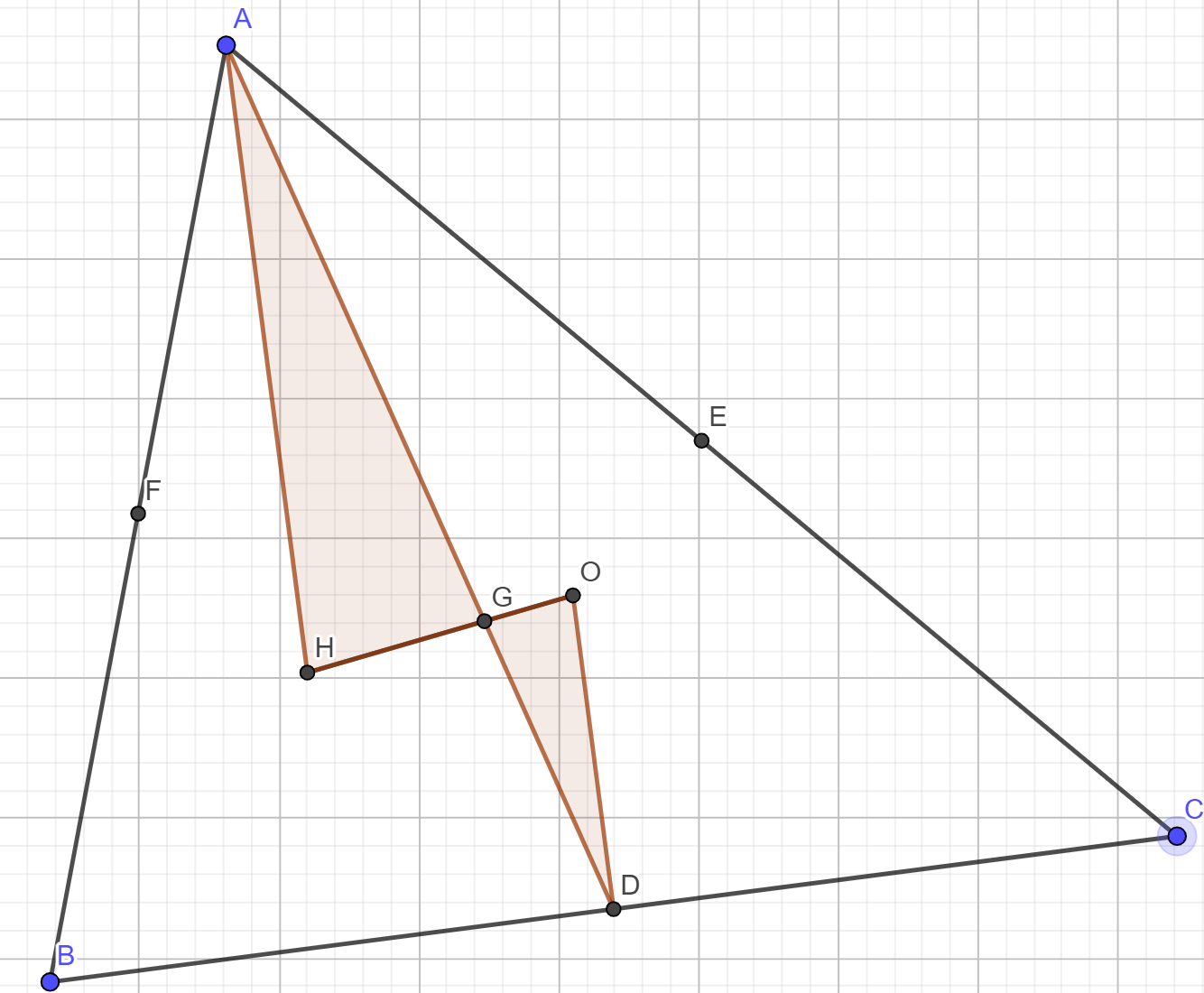
Note you should be able to interact with this diagram (drag around A, B, and C to see how things change) here: https://www.geogebra.org/classic/u6cvqtvp

As an example, to show that H is perpendicular to BC consider the triangles GDO and GAH. G is the centroid, so $AG : GD = 2 : 1$, and therefore $\triangle GAH \sim \triangle GDO$ using SAS. Thus, $\angle GDO = \angle GAH$ so since OD is perpendicular to BC, so is AH. Thus, H is on the altitude from A.

A similar argument can be used to show H is on the altitudes from B and C as well. Hope this helps!