Online Course Discussion Forum
MC II-A Q4.17
I don't get how to do question 4.17, when I use the area formulas, I either come up with an imaginary answer, or an answer that does not make sense for the question. If anyone can offer a hint, that'd be awesome!
What is a little confusing is that in order to include nice numbers, we used approximations. Expanding on this:
The aim of the problem is to use the formula that $[ABC] = abc/4R$ where $R$ is the circumradius. This gives $\displaystyle 20 = \frac{a\cdot 10\cdot 10}{4\cdot 5}$ so solving for $a$ we get $a=BC=4$. The careful student will note that using Heron's formula we then have an area of $8\sqrt{6}\approx 19.5959 \approx 20$.
If we want the triangle to satisfy $[ABC] = 20$, it is possible to set up equations for $a$ (either using Heron's formula or using the fact that since $ABC$ is isosceles, the median from $A$ divides $BC$ into two right triangles) to calculate that $a=BC = 2(\sqrt{35}-\sqrt{15})$ as shown in the diagram below:
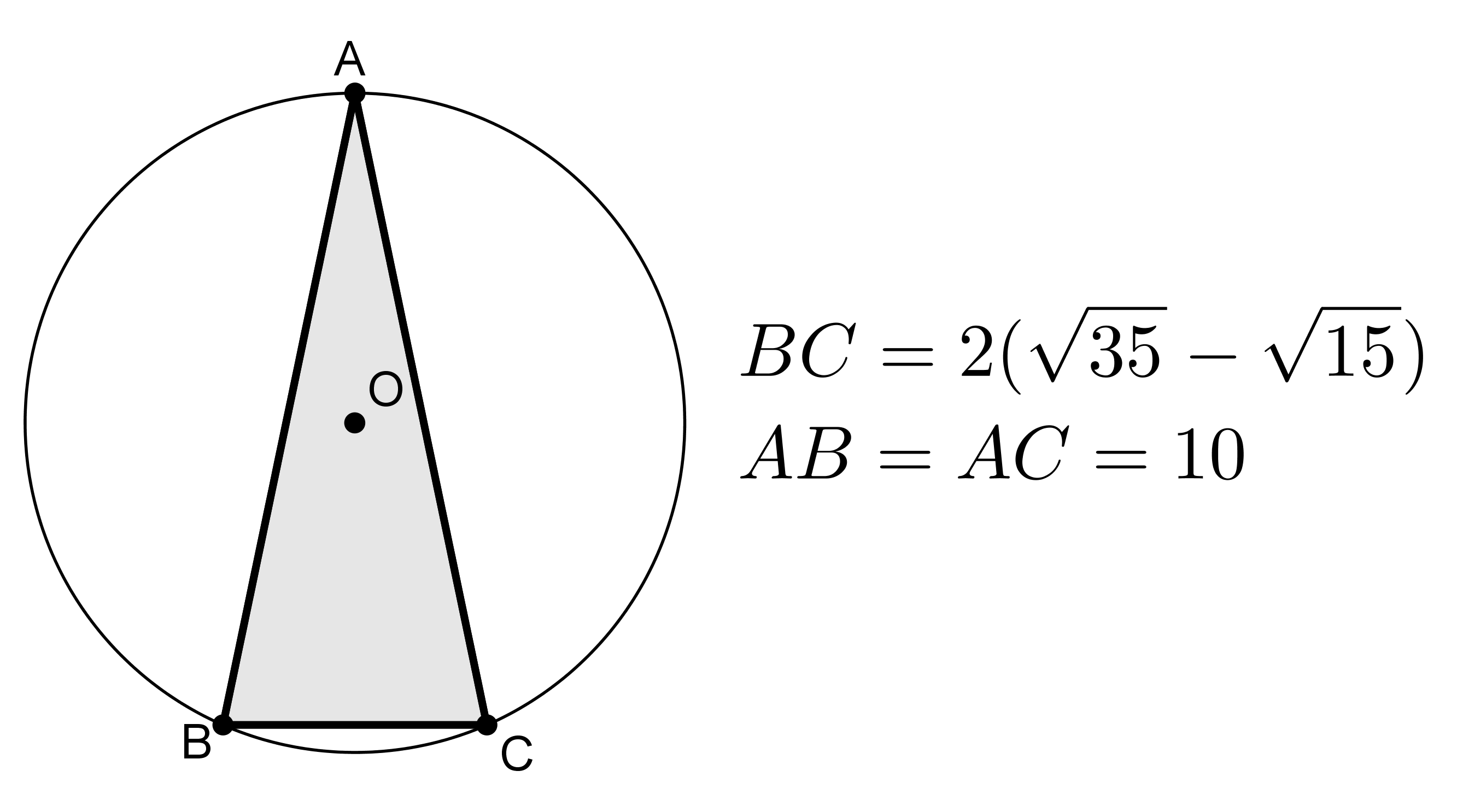
(Caution, calculating $BC$ exactly is not easy.) In this case we get a circumradius $\displaystyle R = \frac{5}{2}(\sqrt{35}-\sqrt{15})\approx 5.108 \approx 5$.
I still don't think this question makes sense because in a circle with radius 5, the diameter is 10, and the diameter is the longest distance on the circle. However, if AB and BC both measure 10, then they are both the diameter, and a triangle can't exist inside a circle if 2 of its sides are the diameter of the circle.
You have a valid point, Grace. If this were the exact measures of the sides of the triangle and the radius, it would be impossible to draw the triangle inside the circle.
Let's take a look at what the radius of a circle with sides $10$, $10$ and $4$ would be. We know from Heron's formula that the area of this triangle is $$\sqrt{12(12-10)(12-10)(12-4)} = \sqrt{384} = 8\sqrt{6}\approx 19.59\approx 20.$$ Using the formula $$[ABC] = \frac{abc}{4R},$$ we can solve for the radius of the circle $$8\sqrt{6} = \frac{(10)(10)(4)}{4R}\Rightarrow R = \frac{100}{8\sqrt{6}} = \frac{25}{2\sqrt{6}} \approx 5.1\approx 5$$
So, a triangle with sides $10$, $10$ and $4$, which has area close to $20$ can be inscribed in a circle of radius a little bit more than $5$. Note how the triangle in the figure on the previous post is thin, and the long sides are almost as long as the diameter of the circle.
Social networks