Online Course Discussion Forum
MCIII Number Theory 5.20, 5.23, 5.27, and 5.28
Hello!
5.20: A little bit stuck, here's what I tried to do:
n^2+5n+16-169k=0 then fixing values for k and then I tried fixing values for n.
I also tried factoring: (n+4)^2-3n=169k
5.23: I tried some factoring like (n-1)(n+1)(n^2+1)(n^4+1)<1 which means n=1 right?
5.27: I got (x-2)(x-5)(x-5)(x-5)=4 works, so x=a+4=b+1=c+1=d+1. But that's not correct, why though?
5.28: Here is what I did:
So that means n=1 (since -x corresponds to -x^n) or -x^n corresponds to something else, namely -x^(nm+1) then -x^(m+1) would correspond to -x since exponents cannot change the sign of the expression, as in no integers k exist such that x^k=-x^k for all x. Then m=0 but m has to be positive.
So that means n must equal to 1 and plugging in n=1 gives m=any positive integer.
What did I do wrong?
Thank you,
Tina Jin
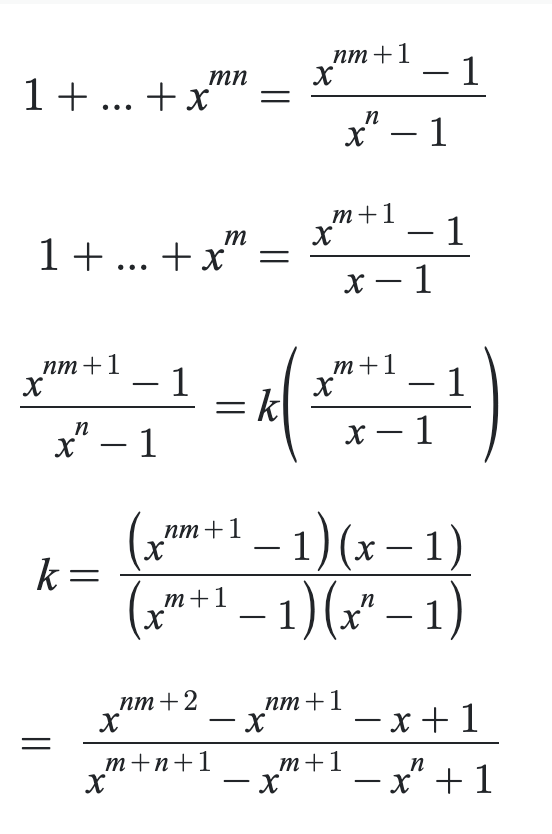
The first fraction is not correct. The numerator should be $x^{n(m+1)}$ instead of $x^{nm+1}$. There is a big difference.
This problem is question number 1 in USAMO 1977. The solution:
Let \[ P(x) = \frac{1+x^n+x^{2n}+\cdots+ x^{mn}}{1+x+x^2 + \cdots + x^m} = \frac{(x^{(m+1)n}-1)(x-1)}{(x^n-1)(x^{m+1}-1)}. \] For all positive integers $m$ and $n$, $x^n-1$ and $x^{m+1}-1$ are both factors of $x^{(m+1)n}-1$. So as long as $x^n-1$ and $x^{m+1}-1$ do not have common factor (or common roots of unity) other than $x-1$, $P(x)$ is a polynomial with integer coefficients. On the other hand, if $x^n-1$ and $x^{m+1}-1$ have a common factor other than $x-1$, it means the equations $x^n-1=0$ and $x^{m+1}-1=0$ have common roots other than $x=1$, but the equation $x^{(m+1)n}-1=0$ has no repeated roots, so in this case $P(x)$ is not a polynomial.\\ Therefore the polynomials $x^n-1$ and $x^{m+1}-1$ do not have any common factor besides $x-1$, in other words, $\gcd(m+1, n)=1$.
5.20: Since $169=13^2$, you can try to analyze in mod 13 first.
5.23: This doesn't look like the correct question. What is the actual question?
5.27: How do you write $4$ as a product of four distinct integers?
5.28: Be very careful to read the question. Especially the numerator polynomial.
I still need some help/hints on these problems.
5.20: I tried analyzing in mod 13, I tried adding and subtracting numbers to make it factorable, but then I guessed and checked a little bit and got some solutions for congruent to 0 mod 13, and I'm not sure how many solutions are congruent to 0 mod 169.
5.21: I believe that is the right question about the function f(n) < or >n. Here is my work:
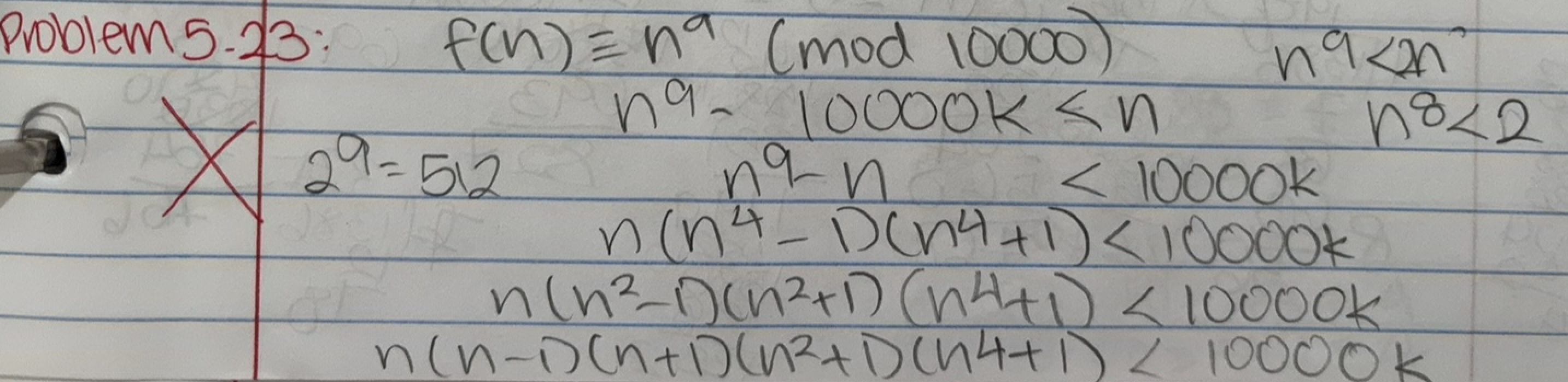
5.27: (-1)(1)(2)(-2) so the answer should be x=a-1=b+1=c+2=d-2, which is still not correct. Why?
5.28: The numerator polynomial should be (x^(nm+n)-1)/(x^n-1), but that gives the conclusion that n=1 and m can be any integer. Why is the answer 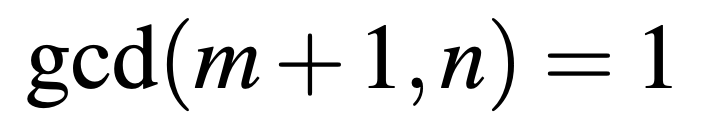 then?
then?
Thanks!
Tina Jin
5.20: Analyze mod 13 first. Testing $n^2+5n+16$ for $n=0,1,2,3,\ldots,12$, we can see that only $n\equiv 4\pmod{13}$ can make $n^2+5n+16$ a multiple of $13$. (Alternatively, to avoid testing out the numbers $0,1,2,3,\ldots,12$ by brute force, you can rearrange the terms to get $n^2+5n+16 = (n-4)^2 + 13n$, and this means $n\equiv 4\pmod{13}$.)
Since $n-4$ is a multiple of $13$, we plug in $n=13k+4$, and then $n^2+5n+16 = 169k^2 + 169k + 36$, and this is not a multiple of $169$. Therefore, there is no solution.
5.23: The question defines a function $f(n)$ to be the last 4 digits of $n^9$, for $n < 10000$. Then compare an odd number $n$ and $f(n)$ (note that both are odd). The question is: for odd numbers below $10000$, which occurs more: $n > f(n)$ (this is set $A$), or $n < f(n)$ (this is set $B$)? First we may consider, are there cases where $f(n)=n$? Obviously $n=1$ is one of the equality cases. Are there more? If you think carefully, $n=9999$ is another, because $9999\equiv -1\pmod{10000}$, and $(-1)^9\equiv -1\pmod{10000}$. Those values correspond to the factors $n-1$ and $n+1$ in the factorization of $n^9-n$. Are there more? From the factorization, it doesn't look like there are more equality cases. However, those two values add up to $10000$, and perhaps we can also look at the other numbers in pairs.
So for odd number $a$, consider $b = 10000-a$. Then $a+b=10000$. We also know that $a^9 + b^9$ has a factor $a+b$. Since $a+b=10000$, we have $10000 \mid a^9+b^9$. That means, $f(a) + f(b) \equiv 0\pmod{10000}$. But we can also see that $f(a)+f(b)$ is not $0$, so it must be that $f(a)+f(b) = 10000$.
Based on the above analysis, if $a > f(a)$, then $b < f(b)$. Therefore, the numbers in $A$ and $B$ are actually matched up, and that means these two sets have the same number of elements.
Social networks