Online Course Discussion Forum
MCIII Algebra 1.26 and 1.31
Hello!
1.26: I only got x=2000, but the answer key says 4,000,000 which just so happens to be my answer squared. How to solve the problem to get 4,000,000 as the answer?
1.31: I got x>3 or x<0 since it solves the inequality
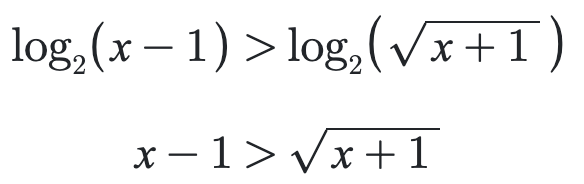
squaring both sides (it is valid to square both sides because both sides are greater than or equal to 0)
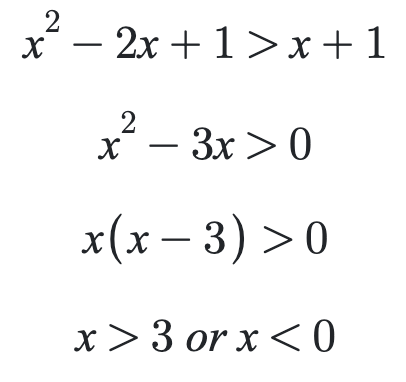
What's wrong with my solution?
Thanks,
Tina Jin
1.26: Please show your solutions. Otherwise how do we find out where you made a mistake? :-) There is always one thing you can do to check your answer. Plug in the value of $x$ back to the equation. Does it work? If it does, then you found a solution. If not, then you made a mistake somewhere.
1.31: The question is: Solve the inequality $$\dfrac{1}{\log_2(x-1)} < \dfrac{1}{\log_2\sqrt{x+1}}.$$
The first thing to do in this kind of questions (equations or inequalities involving logarithm, fractions, and radicals) is to check the domains. For what values of $x$ is the inequality defined? In this question, we need to check the following: (1) denominators cannot be $0$; (2) The quantities to take logarithm should be positive; (3) The quantity inside square root should be nonnegative. Do this before trying to solve anything.
So we have: (1) $\log_2(x-1)\neq 0$ and $\log_2\sqrt{x+1}\neq 0$; (2) $x-1 > 0$ and $\sqrt{x+1} > 0$; (3) $x+1\geq 0$. From (1), $x\neq 2$ and $x\neq 0$. From (2), $x > 1$ and $x > -1$, which means $x > 1$. Here (3) is not a problem any more because (2)'s solution has already taken care of it.
Now, it is time to actually solve the inequality: from the above analysis of the domain of definition, $x\neq 2$ and $x > 1$, so we need to consider two intervals: $1 < x < 2$ and $x > 2$.
If $1 < x < 2$, $0 < x-1 < 1$, so $\log_2(x-1) < 0$. We also have $2 < x+1 < 3$, and thus $\sqrt{x+1} > \sqrt{2} > 1$, which means $\log_2\sqrt{x+1} > 0$. The left hand side is negative and the right hand side is positive, so the inequality is always true in this interval (reciprocals do not change this result). Therefore $1 < x < 2$ is a solution.
If $x > 2$, both sides are positive, then your solution applies. At the end, you got $x > 3$ or $x < 0$, but since we are discussing within the constraint $x > 2$, the part of solution $x < 0$ is extraneous, therefore we only have $x > 3$.
Combining both cases, the full solution is the union of intervals $(1,2)\cup(3,+\infty)$.
Social networks