Online Course Discussion Forum
MCIII Algebra 1.26 and 1.31
Here is my solution to this question, where I got 2000, not 4,000,000:
Why is it wrong?
For 1.31, I got x>3, but why is that wrong?
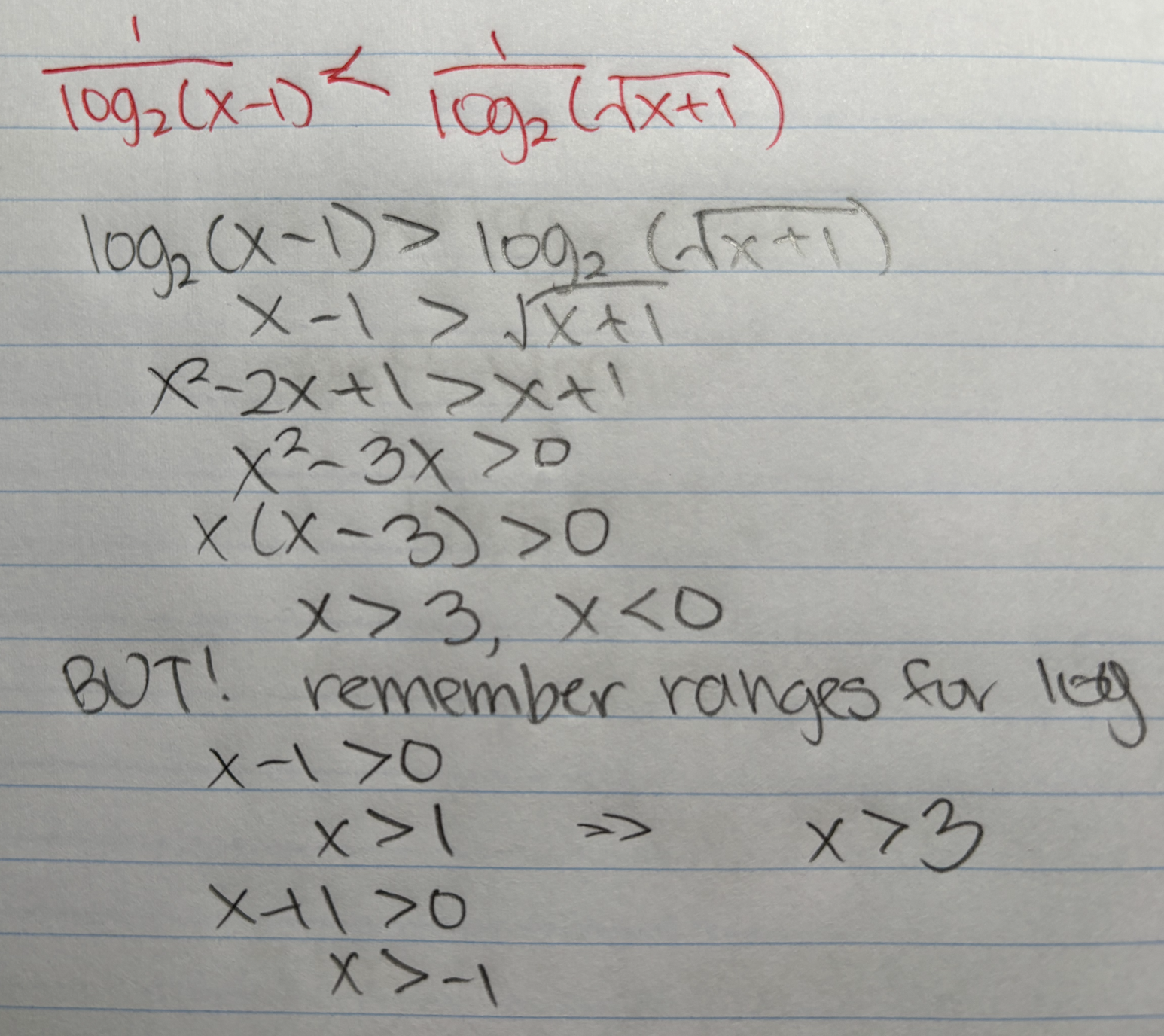
Additionally, if you plug in 1.5 (which is between 1 and 2, as the solutions say), it doesn't work. (1.5-1)=0.5, and sqrt(1.5+1)>1>0.5, so 0.5 is not > 1.5+1, so 1/ log(0.5) is not less than 1/(log(sqrt(x+1)).
Thank you,
Tina Jin
1.26: between your 3rd line and 4th line, $1/2$ became $1$ ...
1.31: Note that $\log_2 0.5 = -1$. Do you see it now?
1.26: The equation the becomes 2y^2-4y+1=0, which still doesn't give the answer of 4,000,000
1.31: Oh! I forgot about the negatives! I got 1<x<2 or x>3 as my final answer.
Tina Jin
1.31 is right.
1.26: The question asks for the product of the positive roots of $x$. Well, all roots of $x$ are positive. The equation you have is $$2y^2 - 4y + 1 = 0,$$ where $y=\log_{2000}x$.
There are two roots for $y$, which means there are two roots for $x$ as well. By Vieta's formula, $y_1 + y_2 = 4/2 = 2$. So it means $$\log_{2000}x_1 + \log_{2000} x_2 = 2.$$ This is the same as $$\log_{2000}(x_1x_2)=2,$$ So $$x_1x_2 = 2000^2=4000000.$$
Social networks