Areteem: MCIII Algebra 5.12

Online Course Discussion Forum

MCIII Algebra 5.12

Hello,

I don't understand why I got this one wrong. I got no solutions. What did I do wrong?

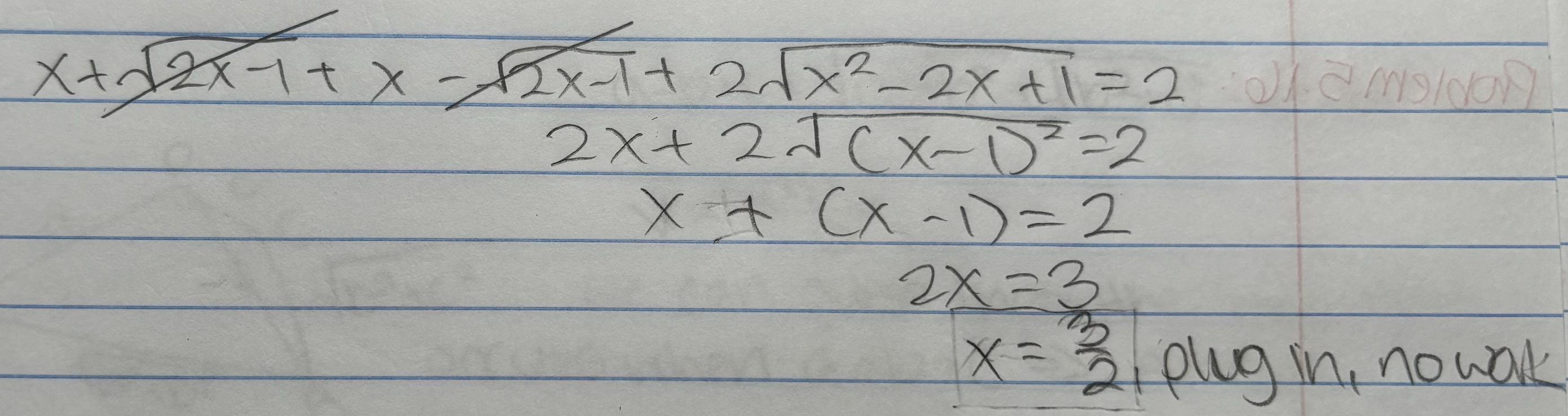
Thanks!

Tina Jin

There are two errors. (1) From the second line to the third line, when you cancel the 2 on the left hand side, you should do the same on the right hand side.

(2) $\sqrt{(x-1)^2} = |x-1|$, not simply $x-1$. Depending on whether $x \geq 1$, it is $x-1$ or $1-x$.

Note that this equation has infinitely many solutions, including every value in the interval $\left[\dfrac{1}{2},1\right]$. This was a problem in the very first IMO in 1959.

Show parent

I still have one question though, when there is an absolute value, say |x-k|, to find the ranges of the cases of the sign of the absolute value, would it be (x>k, x≤k) or is it (x≥k, x≤k), because in this problem it has to be (x≥k, x≤k) for it to achieve both values of 1/2 and 1.

Show parent

As long as the equal sign is included in one of the cases, it is fine.

For the question, you get an equation $x + |x-1|=1$, and there are two cases: (1) $x > 1$; (2) $x\leq 1$. In case (1), you get $x=1$, but that is not in the range, so there's no solution. In case (2), you get an identity $1=1$, which means all $x\leq 1$ are solutions. However, the term $\sqrt{2x-1}$ in the equation requires that $x \geq 1/2$, therefore the final solution is $1/2 \leq x \leq 1$.

Show parent