Online Course Discussion Forum
MCIV
Hello,
I have some quick questions for the MCIV course.
1. Is there an answer key that I could use to check my answers? Not all of the homework problems are reviewed in the class, so I would really appreciate it if I could see what I got right and wrong on the problems I did. (it doesn't show on the grading of the homework, either)
2. For non-homogeneous recurrence relations, I'm unsure where to put the "particular solution". For example, in example 9 of chapter 9 that we did in class, the teacher set a_n=k1*n+k0, but then after plugging that into the given recurrence relation, we got k1=-1, k2=-2. However, now the a_n is somehow not just k1*n+k0, but also c*2^n+k1*n+k0. If a_n=c*2^n+k1*n+k0 the whole time, then why didn't we plug that into the given recurrence relation instead? (the c*2^n comes from solving the characteristic equation x-2=0)
3. For the same packet, in the section ![]() , it says
, it says 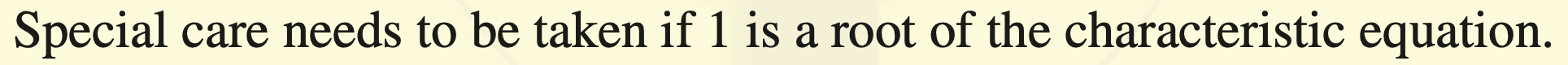
What "special care" needs to be taken?
Thank you and hope you have a great day!
Tina Jin
1. I'll try to provide answer keys in class for questions looking for answers. If it is a proof question, I'd still like you to work on the problems by yourself.
2. Any solution to the homogeneous equation will cancel out when plugged in to the left hand side, so there is no need to have them when we are finding the particular solution.
3. When $1$ is a root of the characteristic equation, it means a constant ("$1^n$") is a solution for the homogeneous version of the recursion. Therefore you will not have a constant in the particular solution for the non-homogeneous one, and thus an "$n$" should be multiplied on the formula for the particular solution before applying the method of undetermined coefficients.
Social networks