Online Course Discussion Forum
Problem 4.39
This is in the book Math Challenge III Combinatorics.
There are multiple ways to calculate the sum. For example, you can start with $S=\{1\}$, and see what answer you get; then let $S=\{1,2\}$, and so on, and check if you get a pattern. Another way to look at it is that you first count how many subsets $S$ has. It is $2^n$. Then there are $2^n$ choices for $A$ and $2^n$ choices for $B$. Focus on one element of $S$, for example $1$. The number $1$ belongs to exactly half of the subsets of $S$. Pick any randomly chosen subset $A$ and another randomly chosen subset $B$, consider the subsets $A\cap B$, $A\cap\overline{B}$, $\overline{A}\cap B$, and $\overline{A}\cap\overline{B}$. (Here $\overline{A}$ means the complement of $A$ with respect to $S$.) How many of these sets contain $1$? From there you can continue to figure out the answer.
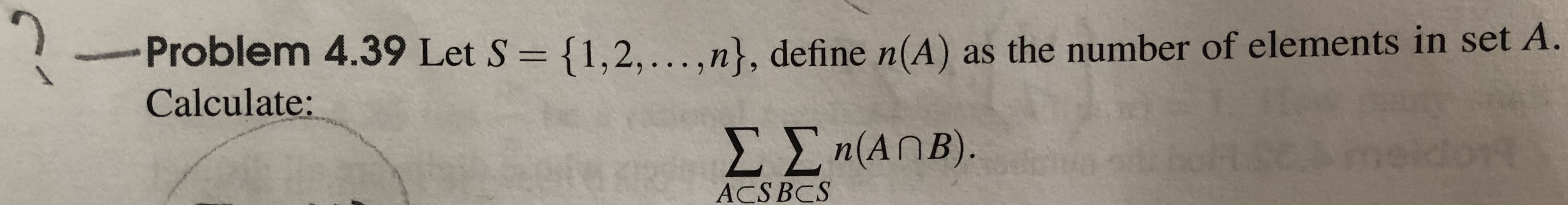
Social networks