Online Course Discussion Forum
MCIV Chapt9 Exmpl 19
Hello,
For example 19, the correct recurrence relation is a_(n+1)=n*a_(n-1)+n*a_n, but I got a_n=(n-1)a_(n-1) (as shown in my solution below).
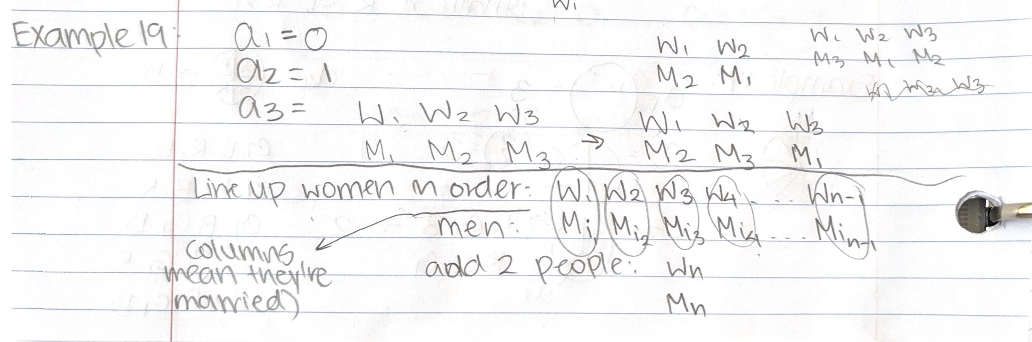

How did the teacher get a_(n+1)=n*a_(n-1)+n*a_n? What is wrong with my reasoning?
Additionally, the teacher eventually got the "Taylor Series" as the answer. Why is the result of that an approximation of e^(-1)?
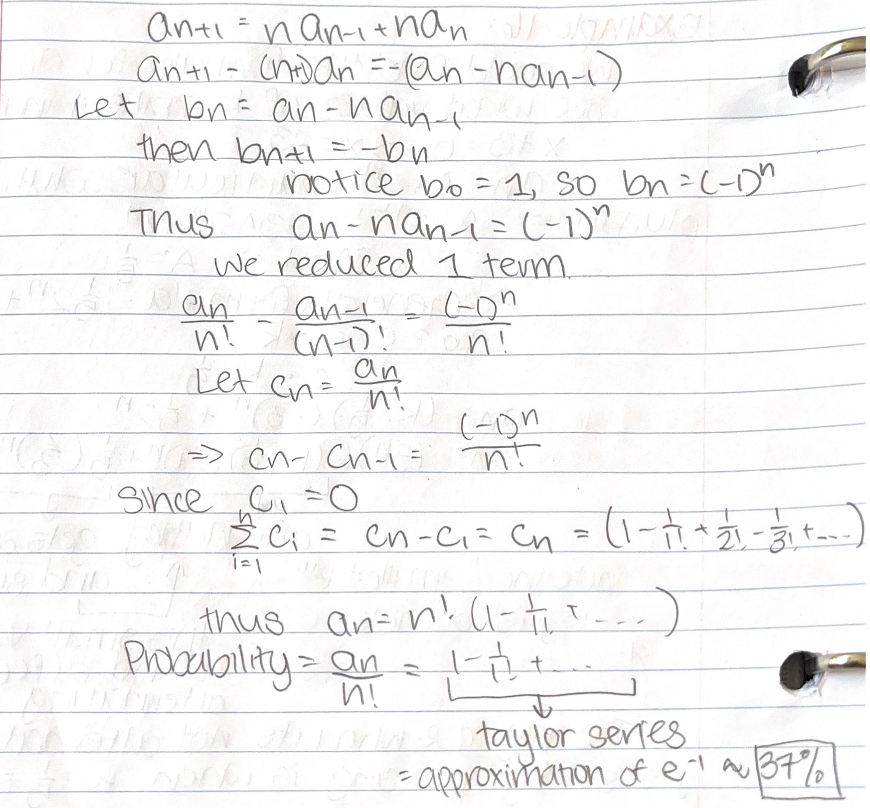
Thank you!
Tina Jin
The part of $(n-1)a_{n-1}$ is correct.
However, the case we considered was about $W_j$ and $M_{i_j}$ are married and $i_j \neq j$. One more case of mismatch for all the $n$ couples is that the two couples $W_n$, $M_n$, $W_j$, and $M_j$ have a swap, and the remaining $n-2$ pairs have $a_{n-2}$ possible mismatches. There are $n-1$ choices for $j$, so this gives $(n-1)a_{n-2}$ choices. Putting together, we have
$$a_n = (n-1)a_{n-1} + (n-1)a_{n-2}.$$
The Taylor series for the function $e^x$ is the following:
$$e^x = 1 + x + \frac{x^2}{2!} + \cdots + \frac{x^n}{n!} + \cdots$$
Our solution (the limit case) is the result when $x=-1$.
Hello Dr. Wang,
Thank you for your reply! I still don't understand how if the two couples Wn, Mn, Wj and Mj have a swap, then it is a separate case. For my solution, isn't that what I did already? If we have another swap, then one of the women, Wn or Wj will be out of order in their line because I defined the top row of women to be increasing in their subscript to avoid overcount.
I am still a little confused on what the second case/part of the recursive sequence is and why.
Thank you,
Tina Jin
There are two cases. In your solution the two cases are not clearly separated, probably because you didn't realize the two cases. Let me explain the two cases, hopefully more clearly.
Suppose we already have the number of mismatches for number of pairs below $n$ (that's including $1$ pair through $n-1$ pairs), and that's $a_1, a_2, \ldots, a_{n-1}$. Now let's consider a new pair, $W_n$ and $M_n$. The requirement is that they are not paired up. So let's pair up $W_n$ and $M_j$ for some $j$ (that's $n-1$ cases, but we will multiply that later). Now, who is pairing up with $W_j$ then? Here we get two cases.
Case 1: $W_j$ is paired with $M_n$. Here we have the $n$th pair swapped with the $j$th pair. The remaining $n-2$ pairs will have $a_{n-2}$ ways of mismatching.
Case 2: $W_j$ is not paired with $M_n$. Here, we pretend that $M_n$ takes the place of $M_j$ and we still have the pairs $1$ through $n-1$, and that's $a_{n-1}$ ways of mismatching.
Now we add up the two cases, and multiply each case by $n-1$ to get
$$a_n = (n-1)a_{n-1} + (n-1)a_{n-2}.$$
Hello Dr. Kevin Wang,
Sorry for the late reply! I just checked the discussion forum. Why are we pretending Mn is taking the place of Mj? If Mn takes the place of Mj, then Wj and Mj are a perfect couple, which isn't allowed by the problem.
Also, if Wj is not paired with Mn, then Wj must be paired with Mk for some k. Then who is Mk's original partner going to be paired with?
I'm still a little confused.
Tina Jin
Before we split into Case 1 and Case 2, $W_n$ is already paired with $M_j$.
You have no problem with Case 1, right?
Now consider Case 2. $W_j$ is not paired with $M_n$. We have the following people not paired yet:
Women: $W_1, W_2, \ldots, W_{j-1}, W_j, W_{j+1}, \ldots, W_{n-1}$.
Men: $M_1, M_2, \ldots, M_{j-1}, M_n, M_{j+1}, \ldots, M_{n-1}$.
We want to find the number of mismatches of this group, considering $W_j$ does not pair with $M_n$, it is equivalent to the original $n-1$ pairs and the newcomer $M_n$ is taking the place of $M_j$. There are $a_{n-1}$ ways.
Social networks