Online Course Discussion Forum
MPFG C1
Hello,
For problem 12 in the packet, I don't understand the last few steps. After getting the "matrix" of "z"s, how did you get that that is 49? I listed out the terms explicitly, and I got:
and since z^(-k)=z^(7-k) by seeing the roots on the unit circle, I got that its just 7(z^0+z^1+...+z^6), but then I'm just doing a loop because we got before that z^0+z^1+...+z^6=2/(1-z^7).
Additionally, why is this reasoning wrong:
b/c z+z^2+z^3+...+z^6+z^7=0 by the fact that the sum of the roots is 0, z+z^2+z^3+...+z^6=0-z^7=0-(-1)=1, thus 1+z+z^2+z^3+...+z^6=1+1=2, but the teacher got that it equals 2/(1-z^7). (I understand how the teacher got that, but I just don't understand what is wrong with my reasoning)
Thanks!
Tina Jin
The first part: Can't see what you got there. Was it an image? It probably didn't upload.
The second part: since $z^7 = -1$ for this problem, we don't have $z^{-k} = z^{7-k}$. In fact $z^{-k} = - z^{7-k}$.
Also I don't think I said $1+z+z^2+z^3+z^4+z^5+z^6=\dfrac{2}{1-z^7}$. It is supposed to be $\dfrac{2}{1-z}$.
The third part, also check that $z^7=-1$ by the problem statement.
Hello Dr. Wang,
First part:
My apologies for the image not loading; here it is (hopefully it will load this time):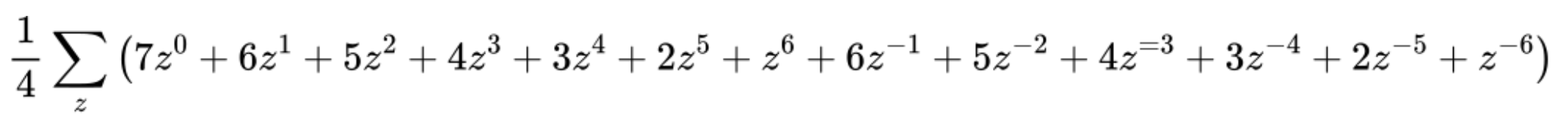
Second part: oops, I get it now, thank you!
Third part: I indeed used z^7=-1, so my reasoning should be correct...but its wrong. What is wrong with my reasoning? (its in the earlier discussion post)
Thank you!
Tina Jin
The image you got is correct. Since $z^7=-1$, the expression for each $z$ is not simplified to $7(z^0+z^1+z^2+\cdots+z^6)$. What we can do here is to calculate the sum over all roots for each term. For the term $7z^0$, we are calculating $7z_1^0+7z_2^0+7z_3^0+\cdots +7z_7^0$, here $z_i$ represents the seven 7th roots of $-1$. This is simply seven $7$s, which sums to 49.
For the other terms, they are all of the form $z^k$ where $k\neq 0$, and we will have
$$z_1^k + z_2^k + \cdots + z_7^k=0,$$
because for a particular fixed $k$, all $z_i^k$ are evenly distributed on the unit circle, since $z_i$ are evenly distributed on the unit circle. Thus the sum is $0$ for this $k$.
Therefore the total sum is $49$.
For the third part, it is still because $z^7=-1$ instead of $1$. Thus the terms $z, z^2, z^3, \ldots, z^6$ are not all roots. Some of them aren't roots of $-1$ (for example, $z^2$ is actually a 7th root of $1$.). Therefore their sum is not $1$.
社交网络